| Code-Phase GPS vs.
Carrier-Phase GPS 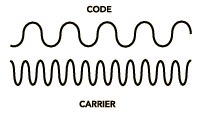
The
words "Code-Phase" and "Carrier-Phase" may sound like electronic
mumbo-jumbo but, in fact, they just refer to the particular signal that we use for timing
measurements. Using the GPS carrier frequency can significantly improve the accuracy of
GPS.
The concept is simple but to understand it let's review a few basic principles of GPS.
Remember that a GPS receiver determines the travel time of a signal from a satellite by
comparing the "pseudo random code" it's generating, with an identical code in
the signal from the satellite.
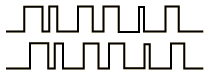
The receiver slides its code later and later in time until it syncs up with the
satellite's code. The amount it has to slide the code is equal to the signal's travel
time.
The problem is that the bits (or cycles) of the pseudo random code are so wide that
even if you do get synced up there's still plenty of slop.
Consider these two signals:
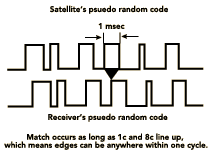
If you compared them logically you'd say they matched. When signal A is a one, signal B
is a one. When signal A is a zero, signal B is a zero.
But you can see that while they match they're a little out of phase. Notice that signal
A is a little ahead of signal B. In fact you could slide signal A almost a half a cycle
ahead and the signals would still match logically.
That's the problem with code-phase GPS. It's comparing pseudo random codes that have a
cycle width of almost a microsecond. And at the speed of light a microsecond is almost 300
meters of error!
Code-phase GPS isn't really that bad because receiver designers have come up with ways
to make sure that the signals are almost perfectly in phase. Good machines get with in a
percent or two. But that's still at least 3-6 meters of error.
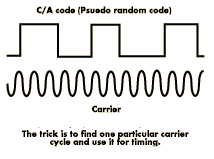
Take it to a higher (frequency) authority
Survey receivers beat the system by starting with the pseudo random code and then move
on to measurements based on the carrier frequency for that code. This carrier frequency is
much higher so its pulses are much closer together and therefore more accurate.
If you're rusty on the subject of carrier frequencies consider your car radio. When you
tune to 94.7 on the dial you're locking on to a carrier frequency that's 94.7 MHz.
Obviously we can't hear sounds at 94 million cycles a second. The music we hear is a
modulation (or change) in this carrier frequency. So when you hear someone sing an
"A" note on the radio you're actually hearing the 94.7 MHz carrier frequency
being varied at a 440 cycle rate.
GPS works in the same way. The pseudo random code has a bit rate of about 1 MHz but its
carrier frequency has a cycle rate of over a GHz (which is 1000 times faster!)
At the speed of light the 1.57 GHz GPS signal has a wavelength of roughly twenty
centimeters, so the carrier signal can act as a much more accurate reference than the
pseudo random code by itself. And if we can get to within one percent of perfect phase
like we do with code-phase receivers we'd have 3 or 4 millimeter accuracy! Yeeow!
Catching the Right Wave
In essence this method is counting the exact number of carrier cycles between the
satellite and the receiver.
The problem is that the carrier frequency is hard to count because it's so uniform.
Every cycle looks like every other. The pseudo random code on the other hand is
intentionally complex to make it easier to know which cycle you're looking at.
So the trick with "carrier-phase GPS" is to use code-phase techniques to get
close. If the code measurement can be made accurate to say, a meter, then we only have a
few wavelengths of carrier to consider as we try to determine which cycle really marks the
edge of our timing pulse.
Resolving this "carrier phase ambiguity" for just a few cycles is a much more
tractable problem and as the computers inside the receivers get smarter and smarter it's
becoming possible to make this kind of measurement without all the ritual that surveyors
go through.
Return |